
Треугольник Паскаля















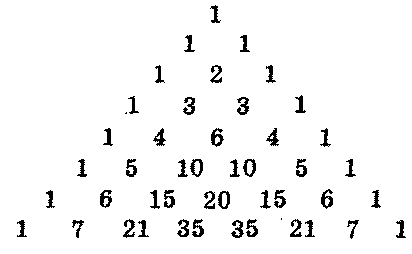




Свойства треугольника Паскаля.
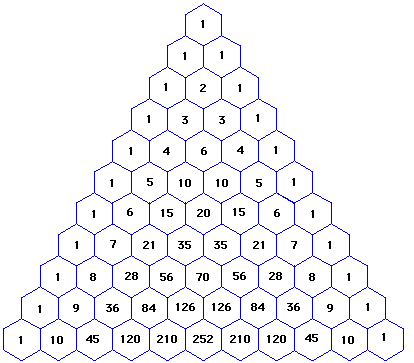
Свойство 1. (основное)
Каждое число равно сумме двух расположенных над ним чисел. Треугольник можно продолжать неограниченно.
Свойство 2.
Первая диагональ треугольника Паскаля – это натуральные числа, идущие по порядку.
Свойство 3.
Вдоль второй диагонали треугольника выстроены треугольные числа (Треугольное число — это число кружков, которые могут быть расставлены в форме правильного треугольника. Очевидно, с чисто арифметической точки зрения, n-е треугольное число — это сумма n первых натуральных чисел) и их обобщения на случай пространств всех размерностей.
Свойство 4.
Третья диагональ треугольника Паскаля - это «пирамидальные» числа или, более точно, тетраэдральные числа, показывающие сколько шаров может быть уложено в виде треугольной пирамиды (тетраэдра).
Свойство 5. (числа Фибоначчи)
Паскаль, наверное, не знал, что числа Фибоначчи скрыты в его треугольнике. Это обстоятельство было обнаружено только в XIX веке — элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, … в которой каждое последующее число равно сумме двух предыдущих чисел). Красным цветом выделены числа Фибоначчи. Сумма чисел n-й диагонали есть n-е число Фибоначчи.
Свойство 6.
Сумма чисел, стоящих на четных местах, равна сумме чисел, стоящих на нечетных местах.
Свойство 7.
Сумма чисел, стоящих в любой строке треугольника, вдвое больше суммы чисел, стоящей в предыдущей строке, поскольку при построении каждой строки числа, стоящие в предыдущей, сносятся дважды.
Свойство 8.
Сумма чисел первой (самой верхней) строки равна 1. Следовательно, суммы чисел, стоящих в строках треугольника Паскаля, образуют геометрическую прогрессию с первым членом, равным 1, и знаменателем 2: 1, 2, 4, 8, ...
Свойство 9.
Каждое число в таблице, будучи уменьшенным на единицу, равно сумме всех чисел, заполняющих пространство, ограниченный теми диагоналям, на пересечении которых стоит это число.
Свойство 10.
Каждое число треугольника Паскаля равно сумме предыдущей диагонали, стоящей над этим числом.
Свойство 11.
Если номер строки треугольника Паскаля – простое число, то все числа этой строки, кроме 1, делятся на это число.
Свойство 12.
Числа, стоящие на горизонтальных строках треугольника Паскаля, - это биномиальные коэффициенты, то есть коэффициенты разложения n (a+b) по степеням.
Свойство 13.
Треугольник Паскаля бесконечен.
Свойство 14.
Сумма чисел в строках треугольника Паскаля = , где n - номер строки.
Свойство 15.
Треугольник Паскаля симметричен относительно центрального столбца.
Свойство 16.
Четвёртая диагональ треугольника Паскаля - это уже фигурные числа в четырехмерном измерении, поэтому это можно только представить в виртуальном мире.
Свойство 17.
Каждое число в таблице, будучи уменьшенным на единицу, равно сумме всех чисел, заполняющих прямоугольник, ограниченный теми вертикальными и горизонтальными рядами, на пересечении которых стоит число А (сами эти ряды в рассматриваемый прямоугольник не включаются).
Свойство 18.
Каждое число А в таблице равно сумме чисел предшествующего горизонтального ряда, начиная с самого левого вплоть до стоящего непосредственно над числом А (в котором клетки, содержащие слагаемые, дающие в сумме А, заштрихованы)
Свойство 19.
В каждой строке треугольника Паскаля сумма чисел на нечётных местах равна сумме чисел на чётных местах.
1+15+15+1=6+20+6
Свойство 20.
Если номер строки треугольника Паскаля – простое число, то все числа этой строки, кроме 1, делятся на это число.
N=5
Числа 5, 10 делятся на 5
Свойство 21.
Если нечётное число в треугольнике Паскаля заменить на точки чёрного цвета, а чётные- белого цвета, то треугольник Паскаля разобьётся на более мелкие треугольники.
Свойство 22.
Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А.
Виды треугольников
Треугольник Тартальи Треугольник Люка
Рассмотрим построенный арифметический треугольник.
Данный треугольник носит название треугольника Люка,
так как суммы чисел, стоящих на восходящих диагоналях,
дают последовательность чисел Люка: 1, 3, 4, 7, 11, 18, /
которые могут быть определены как
Ln=Ln-1+Ln-2, L0=2, L1=1
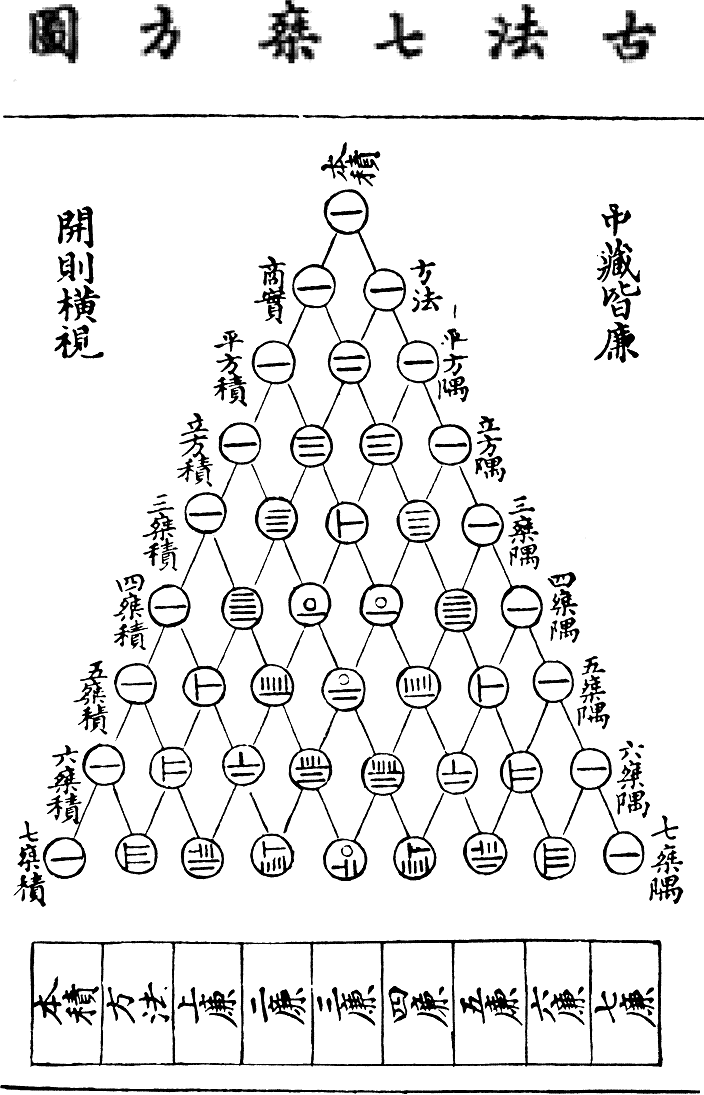
Яшмовое зеркало четырех элементов. Чжу Ши-Цзе.
Рисунок под заголовком «Старинная учебная таблица
из семи умножающихся квадратов» показывает
биномиальные коэффициенты вплоть до восьмой степени.
Треугольник Фибоначчи
Из чисел (fm, n), удовлетворяющих уравнениям fm, n=fm-1,n+fm-2,n, fm, n=fm-1,n-1+fm-2,n-2, где с начальными условиями
f0,0=f1,0=f1,1=f2,1=1 строится следующий треугольник. fm, n =fn fn-m, m Є n Є 0, где fn - n - е число Фибоначчи.
Построенный треугольник назван треугольником Фибоначчи.
Треугольник Трибоначчи
Рассмотрим еще один треугольник, создание которого основано на методе построения треугольника Паскаля. Это треугольник Трибоначчи. Он назван так потому, что суммы элементов, стоящих на восходящих диагоналях, образуют последовательность чисел Трибоначчи: 1,1,2,4,7,13,24,44,..., которая может быть определена следующим рекуррентным соотношением: tn+3 = tn+2 + tn+1 + tn с начальными условиями t0 = 1, t1 = 1, t2 = 2
"Знаковый треугольник"
Построение "знакового треугольника"
Сначала задается первая строка, состоящая из произвольного количества знаков и их расположения. Каждый знак следующей строки получается путем перемножения двух вышестоящих знаков.
Важно заметить, что если постепенно обходить треугольник, то последовательность знаков +, -, -, ... сохранится.
Паскаля треугольник
По краям каждой строки стоят единицы, а каждое из остальных чисел равно сумме двух стоящих над ним чисел предыдущей строки. По этому правилу легко выписывать одну за другой новые строки этого треугольника. Именно в такой форме он приведен в «Трактате об арифметическом треугольнике» французского математика Б. Паскаля (1623-1662), опубликованном в 1665 г.
Паскаля треугольник
Тот же треугольник в «прямоугольной» форме (рис. 4), то целый ряд свойств треугольника Паскаля, связанный с суммами его чисел, будет удобнее наблюдать. В частности, сумма нескольких первых чисел каждого столбца равна идущему за ними числу следующего столбца.




